Найти неопределённый интеграл (множество первообразных или "антипроизводных") означает восстановить функцию по известной производной этой функции. Восстановленное множество первообразных F (x ) + С для функции f (x ) учитывает константу интегрирования C . По скорости перемещения материальной точки (производной) может быть восстановлен закон движения этой точки (первообразная); по ускорению движения точки - её скорость и закон движения. Как видно, интегрирование - широкое поле для деятельности Шерлоков Холмсов от физики. Да и в экономике многие понятия представляются через функции и их производные и поэтому, например, можно по производительности труда в определённый момент времени (производной) восстановить объём продукции, выпущенный в соответствующее время.

Чтобы найти неопределённый интеграл, требуется довольно небольшое количество основных формул интегрирования. Но процесс его нахождения значительно труднее, чем одно лишь применение этих формул. Вся сложность относится не к интегрированию, а к приведению интегрируемого выражения к такому виду, который даёт возможность найти неопределённый интеграл по упомянутым выше основным формулам. Это означает, что для начала практики интегрирования нужно активизировать полученные в средней школе навыки преобразования выражений.

Учиться находить интегралы будем, пользуясь свойствами и таблицей неопределённых интегралов из урока об основных понятиях этой темы (откроется в новом окне).

Существует несколько методов нахождения интеграла, из которых метод замены переменной и метод интегрирования по частям - обязательный джентльменский набор каждого, кто успешно сдал высшую математику. Однако начинать осваивать интегрирование полезнее и приятнее с применением метода разложения, основанном на следующих двух теоремах о свойствах неопределённого интеграла, которые для удобства повторим здесь.

Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.

Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.

(2)

Кроме того, в интегрировании может пригодиться следующее правило: если выражение подынтегральной функции содержит постоянный множитель, то выражение первообразной домножается на число, обратное постоянному множителю, то есть

(3)

Поскольку этот урок - вводный в решение задач интегрирования, важно отметить две вещи, которые либо уже на самом начальном этапе, либо несколько позже могут вас удивить. Удивление связано с тем фактом, что интегрирование - операция обратная дифференцированию и неопределённый интеграл можно справедливо называть "антипроизводной".

Первая вещь, которой не следует удивляться при интегрировании. В таблице интегралов существуют формулы, которые не имеют аналогов среди формул таблицы производной . Это следующие формулы:

Однако можно убедиться в том, что производные выражений, стоящих в правых частях этих формул, совпадают с соответствующими подынтегральными функциями.

Вторая вещь, которой не следует удивляться при интегрировании . Хотя производная любой элементарной функции представляет собой также элементарную функцию, неопределённые интегралы от некоторых элементарных функций уже не являются элементарными функциями . Примерами таких интегралов могут быть следующие:

Для выработки техники интегрирования пригодятся следующие навыки: сокращение дробей, деление многочлена в числителе дроби на одночлен в знаменателе (для получения суммы неопределённых интегралов), преобразование корней в степени, умножение одночлена на многочлен, возведение в степень. Эти навыки нужны для преобразований подынтегрального выражения, в результате которых должна получиться сумма интегралов, присутствующих в таблице интегралов.

Находим неопределённые интегралы вместе

Пример 1. Найти неопределённый интеграл

.

Решение. Видим в знаменателе подынтегрального выражения многочлен, в котором икс в квадрате. Это почти верный признак того, что можно применить табличный интеграл 21 (с арктангенсом в результате). Выносим из знаменателя множитель-двойку (есть такое свойство интеграла - постоянный множитель можно выносить за знак интеграла, выше оно было упомянуто как теорема 3). Результат всего этого:

Теперь в знаменателе сумма квадратов, а это значит, что можем применить упомянутый табличный интеграл. Окончательно получаем ответ:

.

Пример 2. Найти неопределённый интеграл

Решение. Вновь применяем теорему 3 - свойство интеграла, на основании которого постоянный множитель можно выносить за знак интеграла:

Применяем формулу 7 из таблицы интегралов (переменная в степени) к подынтегральной функции:

.

Сокращаем получившиеся дроби и перед нами конечный ответ:

Пример 3. Найти неопределённый интеграл

Решение. Применяя сначала теорему 4, а затем теорему 3 о свойствах, найдём данный интеграл как сумму трёх интегралов:

Все три полученные интеграла – табличные. Используем формулу (7) из таблицы интегралов при n = 1/2, n = 2 и n = 1/5, и тогда

объединяет все три произвольные постоянные, которые были введены при нахождении трёх интегралов. Поэтому в аналогичных ситуациях следует вводить только одну произвольную постоянную (константу) интегрирования.

Пример 4. Найти неопределённый интеграл

Решение. Когда в знаменателе подынтегральной дроби - одночлен, можем почленно разделить числитель на знаменатель. Исходный интеграл превратился в сумму двух интегралов:

.

Чтобы применить табличный интеграл, преобразуем корни в степени и вот уже окончательный ответ:

Продолжаем находить неопределённые интегралы вместе

Пример 7. Найти неопределённый интеграл

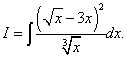
Решение. Если мы преобразуем подынтегральную функцию, возведя двучлен в квадрат и разделив почленно числитель на знаменатель, то исходный интеграл станет суммой трёх интегралов.

Первообразная F(x) от функции f(x) - это такая функция, производная которой равна f(x) :
F′(x) = f(x), x ∈ Δ ,
где Δ - промежуток, на котором выполняется данное уравнение.

Совокупность всех первообразных называется неопределенным интегралом:
,
где C - постоянная, не зависящая от переменной x .

Основные формулы и методы интегрирования

Таблица интегралов

Конечная цель вычисления неопределенных интегралов - путем преобразований, привести заданный интеграл к выражению, содержащему простейшие или табличные интегралы.
См. Таблица интегралов >>>

Правило интегрирования суммы (разности)

Вынесение постоянной за знак интеграла

Пусть c - постоянная, не зависящая от x . Тогда ее можно вынести за знак интеграла:

Замена переменной

Пусть x - функция от переменной t , x = φ(t) , тогда
.
Или наоборот, t = φ(x) ,
.

С помощью замены переменной можно не только вычислить простые интегралы, но и упростить вычисление более сложных.

Правило интегрирования по частям

Интегрирование дробей (рациональных функций)

Введем обозначение. Пусть P k (x), Q m (x), R n (x) обозначают многочлены степеней k, m, n , соответственно, относительно переменной x .

Рассмотрим интеграл, состоящий из дроби многочленов (так называемая рациональная функция):

Если k ≥ n , то сначала нужно выделить целую часть дроби:
.
Интеграл от многочлена S k-n (x) вычисляется по таблице интегралов.

Остается интеграл:
, где m < n .
Для его вычисления, подынтегральное выражение нужно разложить на простейшие дроби.

Для этого нужно найти корни уравнения:
Q n (x) = 0 .
Используя полученные корни, нужно представить знаменатель в виде произведения сомножителей:
Q n (x) = s (x-a) n a (x-b) n b ... (x 2 +ex+f) n e (x 2 +gx+k) n g ... .
Здесь s - коэффициент при x n , x 2 + ex + f > 0 , x 2 + gx + k > 0 , ... .

После этого разложить дробь на простейшие:

Интегрируя, получаем выражение, состоящее из более простых интегралов.
Интегралы вида

приводятся к табличным подстановкой t = x - a .

Рассмотрим интеграл:

Преобразуем числитель:
.
Подставляя в подынтегральное выражение, получаем выражение, в которое входят два интеграла:
,
.
Первый, подстановкой t = x 2 + ex + f приводится к табличному.
Второй, по формуле приведения:

приводится к интегралу

Приведем его знаменатель к сумме квадратов:
.
Тогда подстановкой , интеграл

также приводится к табличному.

Интегрирование иррациональных функций

Введем обозначение. Пусть R(u 1 , u 2 , ... , u n) означает рациональную функцию от переменных u 1 , u 2 , ... , u n . То есть
,
где P, Q - многочлены от переменных u 1 , u 2 , ... , u n .

Дробно-линейная иррациональность

Рассмотрим интегралы вида:
,
где - рациональные числа, m 1 , n 1 , ..., m s , n s - целые числа.
Пусть n - общий знаменатель чисел r 1 , ..., r s .
Тогда интеграл сводится к интегралу от рациональных функций подстановкой:
.

Интегралы от дифференциальных биномов

Рассмотрим интеграл:
,
где m, n, p - рациональные числа, a, b - действительные числа.
Такие интегралы сводятся к интегралам от рациональных функций в трех случаях.

1) Если p - целое. Подстановка x = t N , где N - общий знаменатель дробей m и n .
2) Если - целое. Подстановка a x n + b = t M , где M - знаменатель числа p .
3) Если - целое. Подстановка a + b x - n = t M , где M - знаменатель числа p .

Если ни одно из трех чисел не является целым числом, то по теореме Чебышева интегралы данного вида не могут быть выражены конечной комбинацией элементарных функций.

В ряде случаев, сначала бывает полезным привести интеграл к более удобным значениям m и p . Это можно сделать с помощью формул приведения:
;
.

Интегралы, содержащие квадратный корень из квадратного трехчлена

Здесь мы рассматриваем интегралы вида:
,

Подстановки Эйлера

Такие интегралы могут быть сведены к интегралам от рациональных функций одной из трех подстановок Эйлера:
, при a > 0 ;
, при c > 0 ;
, где x 1 - корень уравнения a x 2 + b x + c = 0 . Если это уравнение имеет действительные корни.

Тригонометрические и гиперболические подстановки

Прямые методы

В большинстве случаев, подстановки Эйлера приводят к более длинным вычислениям, чем прямые методы. С помощью прямых методов интеграл приводится к одному из перечисленных ниже видов.

I тип

Интеграл вида:
,
где P n (x) - многочлен степени n .

Такие интегралы находятся методом неопределенных коэффициентов, используя тождество:

Дифференцируя это уравнение и приравнивая левую и правую части, находим коэффициенты A i .

II тип

Интеграл вида:
,
где P m (x) - многочлен степени m .

Подстановкой t = (x - α) -1 этот интеграл приводится к предыдущему типу. Если m ≥ n , то у дроби следует выделить целую часть.

III тип

Третий и наиболее сложный тип:
.

Здесь нужно сделать подстановку:
.
После чего интеграл примет вид:
.
Далее, постоянные α, β нужно выбрать такими, чтобы коэффициенты при t обратились в нуль:
B = 0, B 1 = 0 .
Тогда интеграл распадается на сумму интегралов двух видов:
;
,
которые интегрируются, соответственно подстановками:
z 2 = A 1 t 2 + C 1 ;
y 2 = A 1 + C 1 t -2 .

Общий случай

Интегрирование трансцендентных (тригонометрических и показательных) функций

Заранее отметим, что те методы, которые применимы для тригонометрических функций, также применимы и для гиперболических функций. По этой причине мы не будем рассматривать интегрирование гиперболических функций отдельно.

Интегрирование рациональных тригонометрических функций от cos x и sin x

Рассмотрим интегралы от тригонометрических функций вида:
,
где R - рациональная функция. Сюда также могут входить тангенсы и котангенсы, которые следует преобразовать через синусы и косинусы.

При интегрировании таких функций полезно иметь в виду три правила:
1) если R(cos x, sin x) умножается на -1 от перемены знака перед одной из величин cos x или sin x , то полезно другую из них обозначить через t .
2) если R(cos x, sin x) не меняется от перемены знака одновременно перед cos x и sin x , то полезно положить tg x = t или ctg x = t .
3) подстановка во всех случаях приводит к интегралу от рациональной дроби. К сожалению, эта подстановка приводит к более длинным вычислениям чем предыдущие, если они применимы.

Произведение степенных функций от cos x и sin x

Рассмотрим интегралы вида:

Если m и n - рациональные числа, то одной из подстановок t = sin x или t = cos x интеграл сводится к интегралу от дифференциального бинома.

Если m и n - целые числа, то интегралы вычисляются интегрированием по частям. При этом получаются следующие формулы приведения:

;
;
;
.

Интегрирование по частям

Применение формулы Эйлера

Если подынтегральное выражение линейно относительно одной из функций
cos ax или sin ax , то удобно применить формулу Эйлера:
e iax = cos ax + isin ax (где i 2 = -1 ),
заменив эту функцию на e iax и выделив действительную (при замене cos ax ) или мнимую часть (при замене sin ax ) из полученного результата.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

4.1. ПРОСТЕЙШИЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 4.1.1. Понятие неопределенного интеграла

В дифференциальном исчислении рассматривалась задача нахождения производной или дифференциала по заданной функции y = F(x), т. е. необходимо было найти f (x) = F"(x) или dF(x) = F"(x) dx = f (x) dx. Поставим обратную задачу: восстановить продифференцированную функцию, т. е., зная производную f(x) (или дифференциал f(x)dx), найти такую функцию F(x), чтобы F"(x) = f (x). Эта задача оказывается значительно более трудной, чем задача дифференцирования. Например, пусть известна скорость перемещения точки, а надо найти закон

ее перемещения S = S(t), причемДля решения подобных

задач вводятся новые понятия и действия.

Определение. Дифференцируемая функция F(x) называется первообразной для функции f (x) на (a; b), если F"(x) = f (x) на (a; b).

Например, для f (x) = x 2 первообразная так как

для f (x) = cos x первообразной будет F(x) = sin x, потому что F"(x) = (sin x)" = cos x, что совпадает с f (x).

Всегда ли существует первообразная для заданной функции f (x)? Да, если эта функция непрерывна на (a; b). Кроме того, первообразных бесчисленное множество, и отличаются они друг от друга только постоянным слагаемым. Действительно, sin x + 2, sin x - 2, sin x + c - все эти функции будут первообразными для cos x (производная от постоянной величины равна 0) - рис. 4.1.

Определение. Выражение F(x) + C, где С - произвольная постоянная величина, определяющее множество первообразных для функции f (x), называется неопределенным интегралом и обозначается символом , т. е., где знак - знак неопределенного

интеграла, f (x) - называется подынтегральной функцией, f (x)dx - подынтегральньм выражением, х - переменной интегрирования.

Рис. 4.1. Пример семейства интегральных кривых

Определение. Операция нахождения первообразной по заданной производной или дифференциалу называется интегрированием этой функции.

Интегрирование - действие, обратное дифференцированию, его можно проверить дифференцированием, причем дифференцирование однозначно, а интегрирование дает ответ с точностью до постоянной. Придавая постоянной величине С конкретные значенияпо-

лучим различные функции

каждая из которых задает на координатной плоскости кривую, называемую интегральной. Все графики интегральных кривых сдвинуты параллельно относительно друг друга вдоль оси Oy. Следовательно, геометрически неопределенный интеграл представляет собой семейство интегральных кривых.

Итак, введены новые понятия (первообразной и неопределенного интеграла) и новое действие (интегрирование), но как все-таки находить первообразную? Чтобы легко было ответить на этот вопрос, надо в первую очередь составить и выучить наизусть таблицу неопределенных интегралов от основных элементарных функций. Она получается в результате обращения соответствующих формул дифференцирования. Например, если

Обычно в таблицу включаются некоторые интегралы, полученные после применения простейших методов интегрирования. Эти формулы помечены в табл. 4.1 символом «*» и доказаны при дальнейшем изложении материала.

Таблица 4.1. Таблица основных неопределенных интегралов

Формула 11 из табл. 4.1 может иметь вид
,

так как. Аналогичное замечание и по поводу фор-

мулы 13:

4.1.2. Свойства неопределенных интегралов

Рассмотрим простейшие свойства неопределенного интеграла, которые позволят интегрировать не только основные элементарные функции.

1.Производная от неопределенного интеграла равна подынтегральной функции:

2.Дифференциал от неопределенного интеграла равен подынтегральному выражению:

3.Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной:

Пример 1. Пример 2.

4.Постоянный множитель можно выносить за знак интеграла: Пример 3.

5.Интеграл от суммы или разности двух функций равен сумме или разности интегралов от этих функций:

Пример 4.

Формула интегрирования остается справедливой, если переменная интегрирования является функцией: если то

Произвольная функция, имеющая непрерывную производную. Это свойство называется инвариантностью.

Пример 5., поэтому

Сравнить с

Универсального способа интегрирования не существует. Далее будут приведены некоторые методы, позволяющие вычислить заданный интеграл с помощью свойств 1-5 и табл. 4.1.

4.1.3.Непосредственное интегрирование

Этот метод заключается в прямом использовании табличных интегралов и свойств 4 и 5. Примеры.

4.1.4.Метод разложения

Этот метод заключается в разложении подынтегральной функции в линейную комбинацию функций с уже известными интегралами.

Примеры.

4.1.5. Метод подведения под знак дифференциала

Для приведения данного интеграла к табличному бывает удобно сделать преобразования дифференциала.

1. Подведение под знак дифференциала линейной функции

отсюда
в частности, dx = d(x + b),

дифференциал не меняется, если к переменной прибавить

или отнять постоянную величину. Если переменная увеличивается в несколько раз, то дифференциал умножается на обратную величину. Примеры с решениями.

Проверим формулы 9*, 12* и 14* из табл. 4.1, используя метод подведения под знак дифференциала:

что и требовалось доказать.

2. Подведение под знак дифференциала основных элементарных функций:

Замечание. Формулы 15* и 16* могут быть проверены дифференцированием (см. свойство 1). Например,

а это и есть подынтегральная функция из формулы 16*.

4.1.6. Метод выделения полного квадрата из квадратичного трехчлена

При интегрировании выражений типа или

выделением полного квадрата из квадратного трехчлена

ax 2 + bx + c удается свести их к табличным 12*, 14*, 15* или 16* (см. табл. 4.1).

Поскольку в общем виде эта операция выглядит сложнее, чем на самом деле, ограничимся примерами.

Примеры.

1.

Решение. Здесь мы выделяем полный квадрат из квадратного трехчлена x 2 + 6x + 9 = (x 2 + 6x + 9) - 9 + 5 = (x + 3) 2 - 4 , а затем используем метод подведения под знак дифференциала.

Рассуждая аналогично, можно вычислить следующие интегралы:

2. 3.

На заключительном этапе интегрирования была использована формула 16*.

4.1.7. Основные методы интегрирования

Таких методов два: метод замены переменной, или подстановка, и интегрирование по частям.

Метод замены переменной

Существуют две формулы замены переменной в неопределенном интеграле:

1) 2)

Здесьсуть монотонные дифференцируемые функ-

ции своих переменных.

Искусство применения метода состоит, в основном, в выборе функцийтак, чтобы новые интегралы являлись табличными или сводились к ним. В окончательном ответе следует вернуться к старой переменной.

Заметим, что подведение под знак дифференциала является частным случаем замены переменной.

Примеры.

Решение. Здесь следует ввести новую переменную t так, чтобы избавиться от квадратного корня. Положим x + 1 = t, тогда x = t 2 + 1, а dx = 2 tdt:

Решение. Заменив x - 2 на t, получим в знаменателе одночлен и после почленного деления интеграл сведется к табличному от степенной функции:

При переходе к переменной x использованы формулы:

Метод интегрирования по частям

Дифференциал произведения двух функций определяется формулой

Интегрируя это равенство (см. свойство 3), найдем:

ОтсюдаЭто и есть формула интегрирования по

частям.

Интегрирование по частям предполагает субъективное представление подынтегрального выражения в виде u . dV, и при этом интеграл должен быть проще, чемВ противном случае применение

метода не имеет смысла.

Итак, метод интегрирования по частям предполагает умение выделять из подынтегрального выражения сомножители u и dV с учетом вышеизложенных требований.

Приведем ряд типичных интегралов, которые могут быть найдены методом интегрирования по частям. 1. Интегралы вида

где P(x) - многочлен; k - постоянная. В этом случае u = P(x), а dV - все остальные сомножители.

Пример 1.

2.Интегралы типа

Здесь положим- другие сомножители.

Пример 2.

Пример 3.
Пример 4.

Любой результат можно проверить дифференцированием. Напр мер, в данном случае

Результат верен.

3.Интегралы вида

где a, b - const. За u следует взять e ax , sin bx или cos bx.

Пример 5.

Отсюда получаем Пример 6.

Отсюда

Пример 7.
Пример 8.

Решение. Здесь надо сперва сделать замену переменной, а потом интегрировать по частям:

Пример 9.
Пример 10.

Решение. Этот интеграл с равным успехом может быть найден как в результате замены переменной 1 + х 2 = t 2 , так и методом интегрирования по частям:

Самостоятельная работа

Выполнить непосредственное интегрирование (1-10).

Применить простейшие методы интегрирования (11-46).

Выполнить интегрирование, используя методы замены переменной и интегрирования по частям (47-74).

Метод разложения

Несколько менее трудоемким является метод, основанный на разложении структуры сети относительно какого-нибудь ее элемента (метод разложения Шеннона-Мура). Идея этого метода заключается в том, чтобы свести анализируемую структуру к последовательно-параллельным соединениям и тем самым избежать полного перебора состояний. Для примера рассмотрим сеть простейшей структуры в виде мостика (рис.2.1).

Рисунок 2.1 Метод разложения

Для простоты положим, что узлы этой сети идеально надежны, а ветви имеют конечную надежность р i , i=. Нумерация ветвей приведена на рисунке. Проделаем с элементом под номером 5 ("перемычка" мостика) два опыта - "короткого замыкания", соответствующий исправному состоянию элемента, и "холостого хода", соответствующий его неисправному состоянию. Если перемычка находится в исправном состоянии, что случается с вероятностью p 5 , то соединяемые ею узлы можно "стянуть" в смысле надежности (см. рис.2.1) и сеть будет иметь вид двух последовательно соединенных и параллельно включенных пар ветвей. Если перемычка находится в неработоспособном состоянии, что случается с вероятностью 1-p 5 , то оставшаяся сеть будет иметь вид параллельного соединения цепочек.

Таким образом, мы "разложили" сеть относительно элемента 5, в результате чего получили две подсети с числом элементов на единицу меньше, чем в исходной сети. Поскольку обе подсети представляют собой последовательно-параллельные структуры, то, пользуясь формулами (2.3) и (2.4), можно сразу записать искомое выражение для вероятности связности сети относительно узлов r, l, используя для компактности обозначениеq i =1-p i .

H rl =p 5 (1-q 1 q 3 ) (1-q 2 q 4 ) +q 5 .

В более сложных структурах может потребоваться неоднократное применение теоремы разложения. Так, на рис.2.2 показано разложение относительно элемента 7 (верхняя строка), а затем по элементу 8 (нижняя строка). Получившиеся четыре подсети имеют последовательно-параллельные структуры и больше не требуют разложений. Легко видеть, что на каждом шаге число элементов в получающихся подсетях уменьшается на единицу а число подсетей, требующих дальнейшего рассмотрения удваивается. Поэтому описанный процесс в любом случае конечен, а число результирующих последовательно-параллельных структур составит 2 m , где т - число элементов, по которым пришлось провести разложение. Трудоемкость этого метода можно оценить величиной 2 m , что меньше трудоемкости полного перебора, но тем не менее все еще неприемлемо для расчета надежности реальных сетей коммутации.

Рисунок.2.2 Последовательное разложение сети

Метод сечений или совокупности путей

Рассмотрим еще один метод расчета структурной надежности сетей. Предположим, как и ранее, что необходимо определить вероятность связности сети между заданной парой узлов A,B. Критерием исправной работы сети в данном случае является наличие хотя бы одного пути передачи информации между рассматриваемыми узлами. Предположим, что имеется список возможных путей в виде перечня элементов (узлов и направлений связи), входящих в каждый путь. В общем случае пути будут зависимы, поскольку любой элемент может входить в несколько путей. Надежность R s любого s-ro пути можно вычислить по формуле последовательного соединения R s =p 1s p 2s …p ts , где p is - надежность i-го элемента s-ro пути.

Искомая надежность H AB зависит от надежности каждого пути и вариантов их пересечений по общим элементам. Обозначим надежность, которая обеспечивается первыми r путями, через H r . Добавление очередного (r+1) - го пути с надежностью R r+1 , очевидно, приведет к увеличению структурной надежности, которая теперь будет определяться объединением двух событий: исправен хотя бы один из первых r путей или исправен (r+1) - й путь. Вероятность наступления этого объединенного события с учетом возможной зависимости. отказов (r+1) - го и остальных путей

H r+i =H r +R r+i -R r+1 H r/ (r+1), (2.10)

где H r/ (r+1) - вероятность исправности хотя бы одного из первых r путей при условии, что исправен (r+1) - й путь.

Из определения условной вероятности H r/ (r+1) следует, что при ее расчете вероятность исправной работы всех элементов, входящих в (r+1) - й путь, необходимо положить равной единице. Для удобства дальнейших расчетов представим последний член выражения (2.10) в следующем виде:

R r+1 H r/ (r+1) = R r+1 ¤ H r (2.11)

где символ (¤) означает, что при перемножении показатели надежности всех элементов, входящих в первые r путей и общих с (r+l) - м путем, заменяются единицей. С учетом (2.11) можно переписать (2.10):

?H r+1 = R r+1 ¤ Q r (2.12)

где?H r+1 =H r+1 -H r - приращение структурной надежности при введении (r+1) - го пути; Q r =1 - H r вероятность того, что произойдет одновременный отказ первых r путей.

Учитывая, что приращение надежности?H r+1 численно равно уменьшению ненадежности?Q r+1 получаем следующее уравнение в конечных разностях:

?Q r+1 =R r+1 ¤ Q r (2.13)

Легко проверить, что решением уравнения (2.13) является функция

Q r = (1-R 1) ¤ (1-R 2) ¤…¤ (1-R r) (2.14)

В случае независимых путей операция символического умножения совпадает с обычным умножением и выражение (2.14) аналогично (2.4) дает коэффициент простоя системы, состоящей из параллельно включенных элементов. В общем случае необходимость учета общих элементов путей заставляет производить умножение согласно (2.14) в алгебраическом виде. При этом число членов в результирующей формуле с умножением на каждый очередной двучлен удваивается и окончательный результат будет иметь 2 r членов, что эквивалентно полному перебору совокупности всех r путей. Например, при r=10 число членов в окончательной формуле превысит 1000, что уже выходит за рамки ручного счета. С дальнейшим увеличением числа путей довольно быстро исчерпываются и возможности современных ЭВМ.

Однако свойства введенной выше операции символического умножения позволяют резко сократить трудоемкость расчетов. Рассмотрим эти свойства более подробно. Согласно операции символического умножения для показателя надежности p i любого элемента справедливо следующее правило:

p i ¤p i =p i . (2.15)

Напомним, что второй сомножитель (2.15) имеет смысл вероятности исправной работы i-го элемента при условии его исправности, которая, очевидно, равна единице.

Для сокращения дальнейших выкладок введем следующее обозначение ненадежности i-го элемента:

=1-p i (2.16)

С учетом (2.15) и (2.16) можно записать следующие простые правила преобразования выражений, содержащих р и р:

p i ¤p i =p i (2.17)

p i p j ¤ =p i p j -p i p s

Для примера использования этих правил при расчете надежности рассмотрим простейшую сеть связи, изображенную на. рис.2.3 Буквы, стоящие у ребер графа, обозначают показатели надежности соответствующих линий связи.

Узлы для простоты будем считать идеально надежными. Предположим, что для связи между узлами А и В можно использовать все пути, состоящие из трех и менее последовательно включенных линий, т.е. следует учесть подмножество путей {м} = {ab, cdf, cgb, ahf}. Определим приращение надежности, обеспечиваемое каждым последующим путем, по формуле (2.12) с учетом (2.14):

Зr+1=Rr+1¤ (¤1¤…¤) (2.18),

Рисунок.2.3 - Пример сети расчета на ограниченном подмножестве путей

Рисунок 2.4 - Пример сети для расчета надежности по полной совокупности путей, где Ri=1-R1 аналогично (2.16).

Применяя последовательно формулу (2.18) и правила символического умножения (2.17). к рассматриваемой сети, получаем

З 2 =cdf¤ () =cdf*;

З 3 =cgb¤ (¤) =cgb**;

З 4 =ahf¤ (¤¤) =ahf**.

При расчете последнего приращения мы использовали правило 4, которое можно назвать правилом поглощения длинных цепей короткими; в данном случае его применение дает b¤cgb=b. Если разрешено использование других путей, например пути cdhb, то не представляет труда рассчитать обеспечиваемое им приращение надежности?H 5 =cdhb¤ (a¤ f¤ g¤ af) = =cdfb*a*f*g. Результирующую надежность сети можно теперь вычислить как сумму приращений, обеспечиваемых каждым из рассмотренных путей:

H R =?H i (2.19)

Так, для рассмотренного примера в предположении, что надежность. всех элементов сети одинакова, т.е. a=b=c=d=f=h=g=p, получаем H 5 =p 2 +p 3 (1-p 2) + +2p 3 (1-p) (1-p 2) +p 4 (1-p) 3 . При машинной реализации в основу расчета можно также положить формулу (2.13), с учетом того, что

Q r =?Q i (2.20)

Согласно (2.13) имеем следующее рекуррентное соотношение

Q r +i =Q r -R r+1 ¤Q r . (2.21)

При начальном условии Q 0 =l на каждом последующем шаге из полученного ранее выражения для Q r следует вычесть произведение надежности очередного (r+1) - го пути на это же выражение, в котором только показатели надежности всех элементов, входящих в (r+1) - й путь, нужно положить равными единице.

В качестве примера рассчитаем надежность сети, изображенной на рис.2.4, относительно узлов А и В, между которыми имеется 11 возможных путей передачи информации. Все расчеты сведены в табл.2.1: перечень элементов, входящих в каждый путь, результат умножения надежности данного пути на значение Q r , полученное при рассмотрении всех предыдущих путей, и результат упрощения содержимого третьего столбца по правилам (2.17). Окончательная формула для q AB содержится в последней колонке, если ее читать сверху вниз. В таблице полностью приведены все выкладки, необходимые для расчета структурной надежности рассматриваемой сети.

Таблица 2.1 Результаты расчета надежности сети, изображенной на рис.2.4

		acmh (b*-d**-rg* *)
		fgmd (*-ac**-rb* *-rc***)	fgmdh (-ac*-rb*-rc*) -
		argmd [*-c**-h* * - f (-c)]
		frcmh (*-ad* *-b* - a* *c-d** *)
		fgmcd [*-r**-d* (-r)]

Для уменьшения объема вычислений не следует без необходимости раскрывать скобки; если промежуточный результат допускает упрощения (приведение подобных членов, вынесение за скобку общего множителя и т.д.), их следует выполнить.

Поясним несколько шагов расчета. Поскольку Q 0 = 1 (при отсутствии путей сеть разорвана), то для Q 1 из (2.21) Q 1 =1- ab=ab. Делаем следующий шаг (6.21) для Q 2 =ab-fghab==ab*fgh и т.д.

Рассмотрим подробнее шаг, на котором учитывается вклад пути 9. Произведение показателей надежности составляющих его элементов, записанное во втором столбце табл.2.1, переносится в третий. Далее в квадратных скобках записана вероятность разрыва всех предыдущих восьми путей, накопленная в четвертом столбце (начиная с первой строки), с учетом правила (2.15), согласно которому показатели надежности всех элементов, вошедших в путь 9, заменяются единицами. Вклад четвертой, шестой и седьмой строк оказывается равным нулю по правилу 1. Далее выражение, стоящее в квадратных скобках, упрощается по правилам (2.17) следующим образом: b =b (fhc-hfc-fhc) =bc (h-fh) =bchf. Аналогично производится расчет относительно всех других путей.

Использование рассматриваемого метода позволяет получить общую формулу структурной надежности, содержащую в рассмотренном случае всего 15 членов вместо максимального числа 2 11 =2048, получающегося при непосредственном перемножении вероятностей отказов этих путей. При машинной реализации метода удобно представить все элементы сети в позиционном коде строкой бит и использовать встроенные булевы функции для реализации логических элементов преобразований (2.17).

До сих пор мы рассматривали показатели структурной надежности сети относительно выделенной пары узлов. Совокупность таких показателей для всех или некоторого подмножества пар может достаточно полно характеризовать структурную надежность сети в целом. Иногда используется другой, интегральный, критерий структурной надежности. По этому критерию сеть считается исправной, если имеется связь между всеми ее узлами и задается требование на вероятность такого события.

Для расчета структурной надежности по этому критерию достаточно ввести обобщение понятия пути в виде дерева, соединяющего все заданные узлы сети. Тогда сеть будет связана, если существует, по крайней мере, одно связывающее дерево, и расчет сводится к перемножению вероятностей отказа всех рассматриваемых деревьев с учетом наличия общих элементов. Вероятность. Q s отказа s-го дерева определяется аналогично вероятности отказа пути

где p is - показатель надежности i-ro элемента, входящего в s-e дерево; n s число элементов в s-м дереве.

Рассмотрим для примера простейшую сеть в виде треугольника, стороны. которого взвешены показателями надежности а, b, с соответствующих ветвей. Для связности такой сети достаточно существования, по крайней мере, одного из деревьев аb, bс, са. Используя рекуррентное соотношение (2.12), определяем вероятность связности этой сети H. cb =ab+bca+cab. Если а=b=с=р, получаем следующее значение вероятности связности, которое легко проверить перебором: H. cb =3р 2 -2р 3 .

Для расчета вероятности связности достаточно разветвленных сетей вместо перечня связывающих деревьев, как правило, удобнее пользоваться перечнем сечений {у} которые приводят к потере связности сети по рассматриваемому критерию. Легко показать, что для сечения справедливы все введенные выше правила символического умножения, только вместо показателей надежности элементов сети в качестве исходных данных следует использовать показатели ненадежности q=1-p. Действительно, если все пути или деревья можно считать включенными "параллельно" с учетом их взаимозависимости, то все сечения включены в этом смысле "последовательно". Обозначим вероятность того, что в некотором сечении s нет ни одного исправного элемента, через р s . Тогда можно записать

р s =q 1s q 2s …q ms , (2.22)

где q is - показатель ненадежности i-ro элемента, входящего в s-e сечение.

Вероятность Н cb связности сети можно тогда представить аналогично (2.14) в символическом виде

Н cb = (1-р 1 ) ¤ (1-р 2 ) ¤…¤ (1-р r ) (2.23)

где r - число рассматриваемых сечений. Другими словами, для того чтобы сеть была связна, необходимо, чтобы одновременно были исправны хотя бы по одному элементу в каждом сечении с учетом взаимной зависимости сечений по общим элементам. Формула (2.23) является в некотором смысле двойственной по отношению к формуле (2.14) и получается из последней заменой путей на сечения и вероятностей исправной работы на вероятности пребывания в состоянии отказа. Аналогично двойственным по отношению к формуле (2.21) является рекуррентное соотношение

H r+1 =H r - р r+1 ¤ H r (2.24)

Рассчитаем для примера вероятность связности рассмотренной выше треугольной сети с набором сечений ab, bc, ca. Согласно (2.23) при начальном условии H 0 =1 имеем H cd =ab-bca-cab. При одинаковых показателях ненадежности элементов сети a=b=c=q получаем H cb =1-q 2 -2q 2 (1 - q). Этот результат совпадает с ранее полученным по методу перечисления деревьев.

Метод сечений можно, конечно, применять и для расчета вероятности связности сети относительно выделенной пары узлов, особенно в тех случаях, когда число сечений в рассматриваемой сети значительно меньше числа нулей. Однако наибольший эффект в смысле сокращения трудоемкости вычислений дает одновременное использование обоих методов, которое будет рассмотрено дальше.

С помощью свойств неопределенного интеграла и таблицы интегралов от элементарных функций становится возможным отыскание первообразных для несложных алгебраических выражений. Например,

В большинстве случае для приведения к табличным интегралам необходимо выполнить предварительное преобразование подынтегрального выражения:

Метод замены переменной

Если подынтегральное выражение является достаточно сложным, то привести его к табличному виду часто удается одним из основных методов интегрирования - методом замены переменной (или методом подстановки ). Основная идея метода состоит в том, что в выражение
вместо переменнойx вводится вспомогательная переменная u , связанная с х известной зависимостью
. Тогда подынтегральное выражение преобразуется к новому виду
, т.е. имеем

.

Здесь, по правилу дифференцирования сложной функции,
=
.

Если, после такого преобразования, интеграл
является табличным или значительно проще исходного, то замена переменной достигла своей цели.

К сожалению, нельзя указать общих правил выбора "удачной" подстановки: такой выбор зависит от структуры конкретного подынтегрального выражения. В разделе 9.12 приводятся примеры, поясняющие различные способы выбора подстановки в ряде частных случаев.

Метод интегрирования по частям

Следующим основным общим методом является интегрирование по частям. Пусть u = u (х) и v=v(x) - дифференцируемые функции. Для произведения этих функций имеем, по свойству дифференциала:

d(uv) = v du + u dv или u dv = d(uv) - v du.

Интегрируя левую и правую части последнего равенства и учитывая свойство 3 неопределенного интеграла, получаем

Эта формула называется формулой интегрирования по частям для неопределенного интеграла. Для ее применения фиксируется разбиение подынтегрального выражения на два сомножителя и и dv. При переходе к правой части формулы первый из них дифференцируется (при нахождении дифференциала: du=u"dx), второй интегрируется:
. Такой прием приводит к цели, если
интегрируется легче, чем
. Пример:

Иногда для получения результата формулу интегрирования по частям приходится применять несколько раз. Отметим, что при промежуточном вычислении
можно не дописывать произвольную постояннуюC ; легко убедиться, что в ходе решения она уничтожится.

Интегрирование рациональных дробей

Если подынтегральная функция представляет собой алгебраическую дробь, то на практике достаточно часто встречаются два типовых случая:

1.Степень числителя дроби больше или равна степени знаменателя (неправильная дробь ). Для такой дроби можно разделить числитель на знаменатель известным из школьного курса методом деления углом (иначе – выделение целой части ), после чего выполнить интегрирование. Пример:

Здесь использовалась и замена переменной:

.

Для промежуточного расчет произвольную С можно не указывать, но в окончательном ответе она обязательна.

2. Метод неопределенных коэффициентов . Если дробь – правильная и знаменатель разлагается на множители, то этот метод позволяет представить подынтегральную функцию суммой простых дробей, проинтегрировать которые уже несложно. Метод имеет большое значение не только в интегрировании. Покажем его суть на примере вычисления интеграла
.

Разложив знаменатель дроби на множители, имеем:
. Введем теперьпредположение , что эту дробь можно представить суммой простых дробей:

Здесь А и В – неизвестные коэффициенты, которые следует найти (неопределенные коэффициенты ). Для этого приведем правую часть равенства к общему знаменателю:

Сократив знаменатели и раскрыв скобки, получим

Теперь используем теорему : чтобы два алгебраических выражения были тождественно равны , необходимо и достаточно равенство их соответственных коэффициентов . Таким образом, получим систему из двух уравнений и решим ее:

.

Следовательно,

.

Возвращаясь к задаче интегрирования, получим